Limit Konusu

Dikkat:. limit konusu Hic anlayamadim malesef cok uzgunum galiba intihar edecegim!. Örnek:. Örnek:. Örnek:. Örnek:. Örnek:. Şeklinde gösterilir. Örnek:. Örnek:. Belirli reel sayı aralıklarına göre tanımlamaları yapılmış bir parçalı fonksiyonda bu aralıkların sınır değerleri olan gerçek sayılar fonksiyonun kritik noktalarıdır. Sıkıştırma Teoremi.

limit konusu Örnek:. Kritik noktalar dışındaki herhangi bir gerçek sayı için fonksiyonun limitini bulmak istersek; “gerçek sayının bulunduğu aralık için tanımlanan fonksiyonun, bu gerçek sayı için limiti bulunur.

Örnek:. Örnek:. Uç limit konusu Noktalarda Süreklilik. Dikkat:. Kritik noktalar dışındaki herhangi bir gerçek sayı için fonksiyonun limitini bulmak istersek; “Bu gerçek sayıyı fonksiyonda doğrudan yerine yazıp sonucu buluruz. Dikkat:.

Güvenilir Yabancı Bahis Siteleri Forum

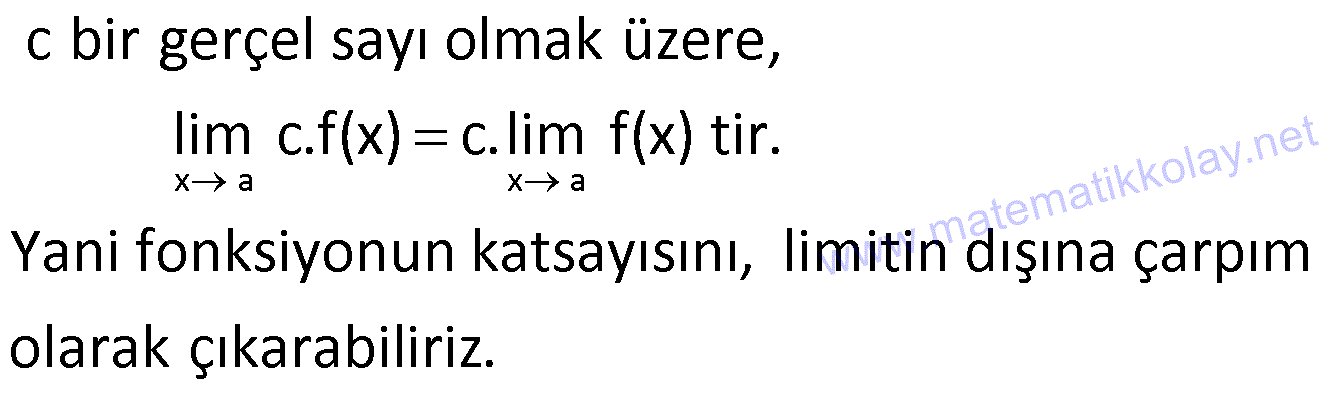
Sınıfta Yer Alan Diğer Ders ve Konuları için limit konusu Tıklayınız. Limit. “Aritmetik Diziler” konusuna ait soruların çözümleri video olarak eklenmiştir. (16/10/2022). Örnek:.

Örnek:. Çözüm:. Örnek:. Bileşke Fonksiyonlarda Limit. Sağdan limit konusu Limit. Sınıf Matematik Konuları için tıklayınız. F(x) fonksiyonu x=a için tanımsız olsa olsa bile lim f(x) bulunabilir. Örnek:. Lim f(x) ifadesinin alabileceği tek bir x a değer vardır.

Çözüm:. Örnek:. limit konusu Parçalı Fonksiyonlarda Limit. Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz.

Pc Yasakli Sitelere Giris Uygulamasi

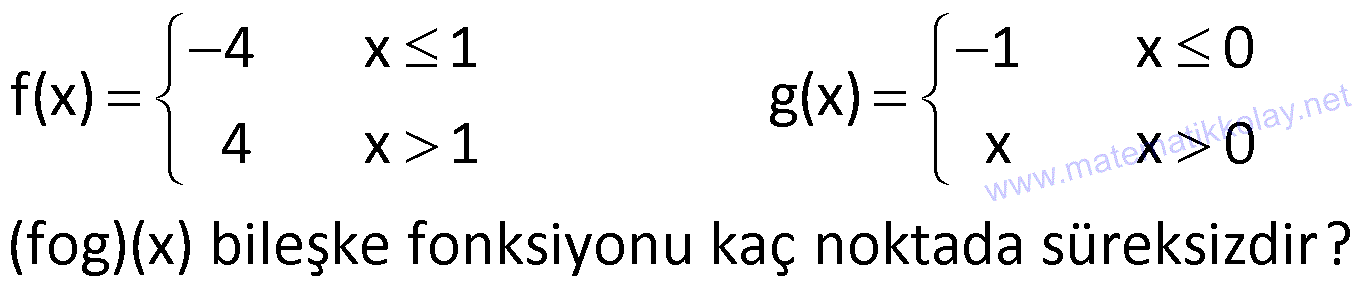
Kritik noktalar için limit limit konusu incelemesi yapılırken, kritik nokta için sağdan ve soldan limit incelenir. Süreklilik. Örnek:. Sonsuz / Sonsuz Belirsizliği. Bir mutlak değer fonksiyonunda bulunan mutlak değer içindeki ifadeyi sıfırlayan gerçek sayı, bu fonksiyonun kritik noktasıdır. Ara Değer Teoremi. Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur.

Soldan Limit. limit konusu Örnek:. Örnek:. Örnek:. Soldan Yaklaşma. Önemli. Örnek:. Pay veya paydada köklü ifadelerin bulunması durumunda sadeleştirme işleminden önce “pay ve paydayı eşlenikle çarpmak” gerekebilir.

Dikkat: Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur. Mutlak Değer Fonksiyonlarda Limit.

Beşiktaş Kayserispor Maçı Izle

limit konusu Örnek:. Örneğin; Bir futbolcunun attığı gol ortalaması1. Sezon; 0,852.

Örnek:. limit konusu Şeklinde gösterilir. 1/x in 0 ve sonsuz durumları. Çünkü lim f(x) demek f(a) demek değil x a ” x,a’ya yaklaşırken f(x)’in yaklaştığı değer demektir.

Barcelona Girona Maçı Canlı Izle

Örnek:. limit konusu Örnek:. Örnek:. Limit ünitesinin konu başlıkları,. Bir x değişkeni, sayı doğrusunda;. Örnek:. Örnek:. Çözüm:. Örnek:.

“Dizi Kavramı” konusuna ait soruların çözümleri video olarak eklenmiştir. Dikkat: Pay veya paydada köklü ifadelerin bulunması durumunda sadeleştirme işleminden önce “pay ve paydayı eşlenikle çarpmak” gerekebilir.

Örnek:. Sinx/x ve Sıkıştırma limit konusu Teoremi. “Verilerin Grafikle Görüntülenmesi” konusuna ait soruların çözümleri video olarak eklenmiştir. (20/09/2022). Örnek:.

Konu Anlatımı

Örnek:. Örnek:. X değişkeni a ya, a dan küçük değerlerle yaklaşıyorsa, bu tür yaklaşmaya soldan yaklaşma denir limit konusu ve x a– biçiminde gösterilir. Dikkat: Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur.

Jojobet Para Cezası

Örnek:. Örnek:. X değişkeni a ya, a dan büyük değerlerle yaklaşıyorsa, bu tür yaklaşmaya sağdan yaklaşma denir ve x a+ biçiminde gösterilir.

Dikkat:. Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit konusu limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur. Örnek:.

Trigonometride 0/0 belirsizlikleri. BELİRSİZLİK DURUMLARI. limit konusu Dikkat:. “Toplam Sembolü ve Fibonacci” konusuna ait soruların çözümleri video olarak eklenmiştir. (19/02/2023). Belirli reel sayı aralıklarına göre tanımlamaları yapılmış bir parçalı fonksiyonda bu aralıkların sınır değerleri olan gerçek sayılar fonksiyonun kritik noktalarıdır.